3-1 Neural network example
1. Neural network의 예시




- Shallow network: 은닉층이 하나인 신경망
- 함수 f: 입력 x와, 출력 y를 매핑하는 파라미터 ϕ를 가짐.
- 파라미터 10개(바이어스 4개, 가중치 6개)
2. 파라미터에 따른 그래프.

- 파라미터의 선택에 따라 서로 다른 형태의 그래프가 나옴.
- input, output 관계가 piecewise linear하게 나옴.
- 그러나 모두 3개의 변곡점을 가지고 있다는 공통점이 있음.
- joint의 수는 노드 수이다!(마지막 hidden layer의 노드 수가 3개여서 3개의 변곡점.)
3. shallow network그래프 그리는 과정
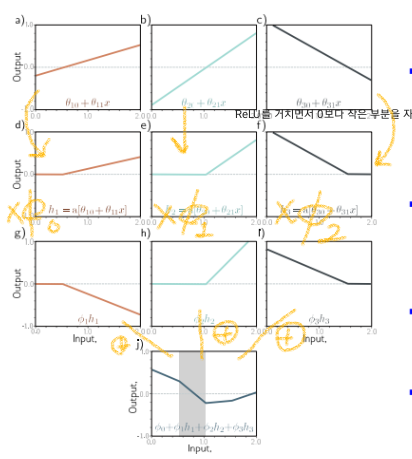
- step1) 0보다 작은 부분을 0으로 만듦.(이때 꺾이는 부분이 최종출력의 joint가 됨)
- step2) 각 노드의 파라미터를 곱해줌
- step3) 세 함수를 더해줌.
- step4) 전체 함수의 높이를 제어하는 파라미터를 더함.
- step1에서 0으로 잘리면(clipped) 활성화가 안 된 것. 안 잘리고 값이 그대로면 활성화 된 것.
- 위의 색칠된 부분은 h1과 h3의 영향을 받음.
- 위의 색칠된 부분의 기울기는 " θ11ϕ1 + θ31ϕ3 "
- ReLU함수를 사용하면 D개의 hidden unit이 있으면 D개의 joint와 D+1개의 linear region을 가짐.
- 즉, hidden units만 충분히 있으면 어떤 그래프도 다 만들 수 있다!!
3-2 Universal approximation theorem(범용 근사 정리)
1. Shallow neural network의 hidden layer 수
: Shallow neural network의 hidden layer 수는 네트워크의 성능(capacity)의 척도임.
2. 범용 근사 정리(Universal approximation theorem)
: hidden unit이 충분하다면, 임의의 연속함수를 만들 수 있다.

3-3 Multivariate inputs and outputs(다변량 입력과 출력)
1. 다변량 출력
: 지금까지 출력노드가 하나인 neural network를 봤다면, 이번에는 다변량 출력(출력 노드 여러개)를 보겠다. 입력 노드는 2개, hidden 노드는 4개, 출력 노드느 2개이다.



2. 다변량 입력

: 입력의 노드가 2개이면 1차원 선 그래프가 아닌, 2차원 평면이 입력된다.

step0) (a)에서 밝기는 θ10 + θ11x1 + θ12x2./ 얇은 선은 등고선을 나타냄.
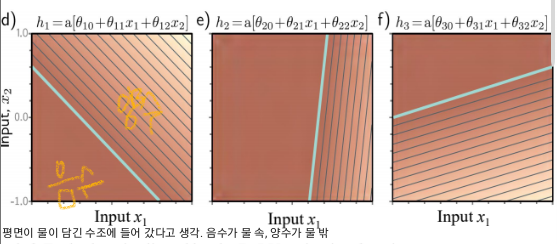
step1) a~c를 ReLU함수에 넣음. 여기서 청록색 부분이 joint 부분이됨.
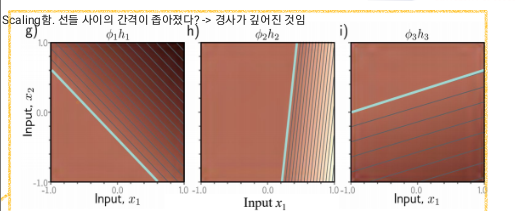
step2) d~f에 각각의 ϕ를 곱함
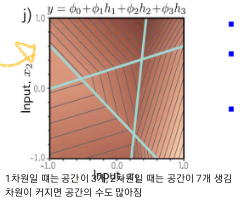
step3) 세 평면을 더함.
step4) 높이를 결정하는 ϕ0를 더함.
- 결과 볼록한 분할 선형 다각형(convex piecewise linear polygonal) 영역으로 이뤄진 표면이 나옴.
- 중앙 삼각형 영역에서 첫번째와 세번째 히든 유닛이 활성화 됨.
- 입력 모델에 2개 이상의 입력이 있으면, 출력은 입력의 연속적 분할 선형함수가 됨.
- 이때 선형 영역은 다차원 입력공간에서 볼록 다각체임.(convex polytopes)
3. 선형 영역 vs 히든 노드
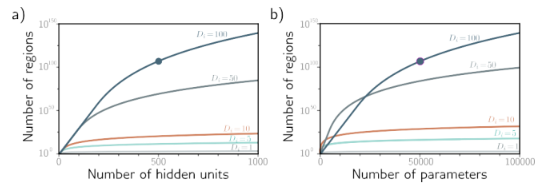
a) D(차원)와 히든 노드 수에 따른, 결과 영역의 최대 수. Di = {1,5,10,50,100}
b) D와 파라미터 수에 따른,결과 영역의 최대 수
4. 선형 영역 vs 입력 차원
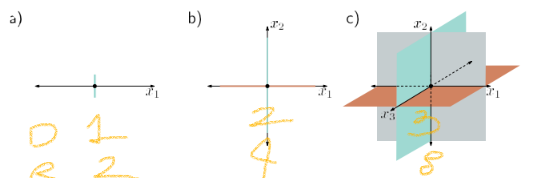
a) 1개 입력(1차원): 2(2^1)개의 선형 영역
b) 2개 입력(2차원): 4(2^2)개의 선형 영역
c) 3개 입력(3차원): 8(2^3)개의 선형 영역
3-4 Shallow neural networks: general case
1. 일반화
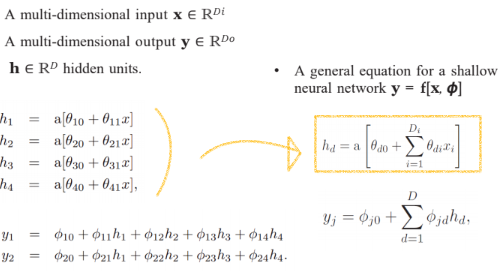
▪ 다차원 입력 x ∈ R^Di
▪ 다차원 출력 y ∈ R^Do
▪ h ∈ R^D 히든 노드.
2. 예시
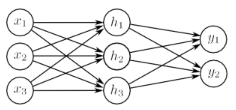
: 20개의 파라미터를 가짐.(3*3 + 3*2 + 5)
: 9 + 6개의 기울기, 6개의 offset.
: ReLU 활성화 함수를 사용하면 네트워크는 입력 공간을, convex polytopes (볼록 다각형)으로 나눔.
3-5 Terminology(용어)
- Pre-activations(z): 히든 레이어의 입력 값. 즉, ReLU함수 적용되기 전.
- Activations: 히든 레이어에서의 값.
- Feed-forward networks: 순환하지 않는 그래프를 만드는 신경망.
- Fully connected:한 레이어의 모든 노드가 다음레이어의 모든 노드에 연결된 경우.
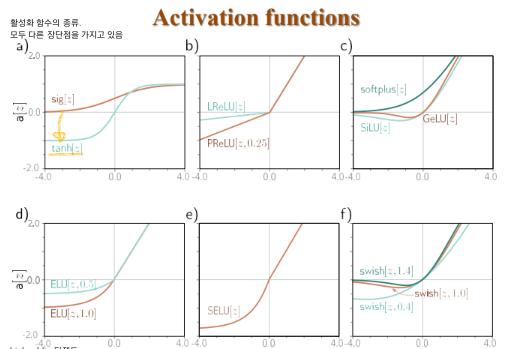
- highpublic 탄젠트/ Leaky ReLU/ Parametric ReLU/ Gaussian error LU/ Exponential LU/ Scaled Exponential LU/ Sigmoid LU/ swish
3-6 Summary
1. Shallow neural network 과정
(i) 입력에 대한 여러 선형 함수를 계산.
(ii) 각 결과를 활성화 함수를 통과시킴.
(iii) 이러한 활성화의 선형 조합을 사용하여 출력을 형성.
→ 입력 공간을 분할하여 분할 선형 영역(초평면된 조각, piecewise linear)의 연속 표면을 형성.
→ Universal approximation theorem: 충분한 노드가 있으면 임의의 연속함수를 근사화할 수 있음.
◆ Shallow network에서 히든 노드의 수는 joint 수이다.
◆ Shallow network에서 출력 노드의 수는 출력 그래프(평면)의 개수이다.
◆ Shallow network에서 입력 노드의 수가 n이면 입력한 형태는 n차원이다.
◆ Shallow network에서 입력 노드의 수가 n이면 2^n개의 선형 영역이 생긴다.
(근데 input값과 output값을 함께 좌표상에 나타낼 때는 n+1차원이 됨!)
'Computer Science > Artificial Intelligence' 카테고리의 다른 글
| [인공지능] SP05. Loss functions (0) | 2023.10.21 |
|---|---|
| [인공지능] SP04. Deep neural networks (0) | 2023.10.18 |
| [인공지능] 6장/ 7장/ 8장 (2) | 2023.10.17 |
| [인공지능] 5장 Training Multi-layer preceptron (0) | 2023.10.01 |
| [인공지능] 4장 Learning: Gradient descent algorithm (2) | 2023.10.01 |



