[자료구조] 3장 Linked List

3-1 리스트

1. 리스트란

: 순서를 가진 항목들의 모임.

2. 리스트의 구조

: 선형의 자료구조(스택, 큐와 공통점). 임의의 위치에서도 삽입과 삭제가 가능함(스택, 큐와 차이점)

3. 리스트 ADT(추상 자료형)

데이터: 임의의 접근 방법을 제공하는 같은 타입 요소들의 순서 있는 모임
연산(9):
⊙ init(): 리스트 초기화.
⊙ insert(pos, item): pos 위치에 새로운 요소 item을 삽입.
⊙ delete(pos): pos 위치의 요소를 삭제.
⊙ get_entry(pos): pos 위치에 있는 요소 반환
⊙ is_empty(): 리스트가 비어 있는지 검사
⊙ is_full(): 리스트가 가득 차 있는지 검사.
⊙ find(item): 리스트 요소 item이 있는지 살핌.
⊙ replace(pos, item): pos 위치를 새로운 요소 item으로 바꿈.
⊙ size(): 리스트 안의 요소의 개수를 반환

3-2 리스트의 구현

배열	연결리스트
구현이 간단	구현이 복잡
삽입, 삭제 시 오버헤드	삽입, 삭제가 효율적
항목의 개수 제한	크기가 제한되지 않음.

1. 배열을 이용해 구현

- 구현

typedef int Element;
Element data[MAX_LIST_SIZE]
int length = 0;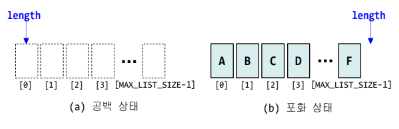

- 연산

(1) 삽입 연산: 삽입위치 다음의 항목들을 이동해야 함.

void insert(int pos, Element e)
{
    if(is_full()==0 && pos>=0 && pos<length)
    {
    	for(int i = length ; i > pos ; i--)
        	data[i] = data[i-1];
        data[pos] = e;
        length++;
    }
    else error("포화 상태 오류 또는 삽입 위치 오류")
}

(2) 삭제 연산: 삭제위치 다음의항목을 이동해야 함.

void delete(int pos)
{
    if (is_empty == 0 && 0<=pos && pos<length)
    {
    	for (int i=pos+1 ; i<length ; i++)
        	data[i-1] = data[i];
        length--;
    }
    else error("공백상태 오류 또는 삭제 위치 오류")
}

2. 단순 연결리스트를 이용해 구현

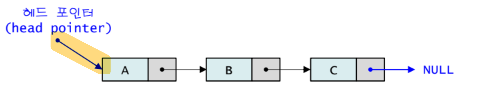
- 구현

typedef struct node_t{
    int data;               // 데이터 필드
    struct node_t* link;   // 링크 필드
}Node;

Node* head = NULL;

: strcut node_t를 Node라는 별칭으로 정의.

: link는 자신과 같은 구조체를 가르키는 포인터

- 연산

(1) 리스트 초기화 연산

void init_list(){ head = NULL;}

(2) empty 확인 연산

int is_empty(){ return head == NULL;}

(3) 특정 위치 요소 반환 연산

Node* get_entry(int pos)
{
    Node* p = head;
    for(int i = 0; i<pos ; i++, p = p->link)
         if(p=NULL){return NULL}
    return p;
}

(4) 크기 반환 연산

int size()
{
    Node* p;
    int count = 0;
    for(p=head ; p!=NULL ; p=p->link)
    	count++;
    return count;
}

(5) 요소 교환 연산

void replace(int pos, int val)
{
    Node* node = get_entry(pos)
    if(node != NULL)
	    node->data = val;
}

(6) 요소 위치 확인 연산

Node* find(int val)
{
    Node* p;
     for( p = head ; p!=NULL ;p=p->link)
         if(p->data == val) return p;
     return NULL;
}

(7) 삽입 연산

void insert_next(Node* before, Node* node)
{
    if(n != NULL){
        node->link = before->link;
        before->link = node;
    }
]

void insert(int pos, int val)
{
    Node* new_node, * prev;
    new_node = (Node *)malloc(sizeof(Node));
    new_node->data = val;
    new_node->link = NULL;
    
    if (pos==0){
        new_ndoe-> link = head;
        head = new_node;
    }
    else{
        prev = get_entry(pos - 1)
        if(prev != NULL)
            insert_next(prev, new_node);
        else free(new_node)
    }
}

(8) 삭제 연산

Node* remove_next(Node* prev)
{
    Node* removed = prev -> link;
    if(removed != NULL)
        prev -> link = removed -> link;
    return removed;
}

void delete(int pos)
{
    Node* prev, * removed;
    if(pos==0 && is_empty()==0){
        removed = head;
        head = head -> link
        free(removed)
    }
    else{
        prev = get_entry(pos-1);
        if (prev != NULL)
            removed = remove_next(prev);
            free(removed);
    }
}

(9) 리스트 비우는 연산

void clear_list()
{
  while (is_empty() == 0)
      delete(0)
}

(10) 리스트 출력 연산

void print_list(char* msg)
{
    Node* p;
    printf("%s[%2d]: ", msg, size());
    for (p = head ; p!=NULL ; p=p->link)
        printf("%2d", p->data);
    printf("\n");
}

(11) 전체 노드의 데이터 합

int sum()
{
    int sum = 0;
    Node* p;
    for(p=head ; p != NULL; p->link)
       sum+= p->data;
    //while (p != NULL) {
	//	    sum += p->data;
	//	    p = p->link;
	// }
    return sum;
}

3. 이중 연결리스트를 이용해 구현

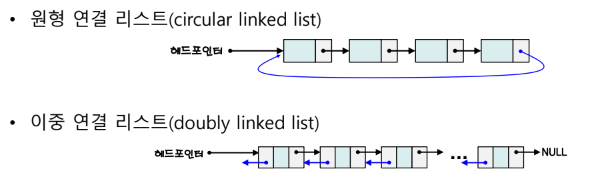
- 구현

typedf struct node_t{
    int data;
    strcut node_t* prev;
    struct node+t* next;
} Node;

Node head;

- 연산

(1) 리스트 초기화 연산

void init_list() { head.next = NULL; }

(2) 헤드 반환 연산

Node* get_head() { return head.next; }

(3) empty 확인 연산

int is_empty() { return get_head() == NULL; }

(4) 특정 위치 요소 반환 연산

Node* get_entry(int pos)
{
    Node* n = &head;
    int i = -1;
    for(i=-1 ; i<pos ; i++, n=n->next)
        if (n == NULL) break;
    return n;
}

▶ 위의 단순연결리스트에서는 head를 첫번째 노드의 주소를 가지고 있는 포인터로 봤지만,

이 코드의 이중연결리스트에서는 head를 하나의 노드로 보고 있기 때문에 i는 -1부터다.

(5) 요소 교환 연산

void replace(int pos, int val)
{
    Node* node = get_entry(pos);
    if (node != NULL)
        node->data = val;
}

(6) 크기 반환 연산

int size()
{
     Node* p;
     int count = 0;
     for( p=get_head() ; p!=NULL ; p=p->next)
         count++;
     return count;
     
}

(7) 요소 위치 확인 연산

Node* find(int val)
{
    Node* p;
    for(p=get_head() ; p!=NULL ; p=p->next)
        if(p->data == val) return p;
    return NULL;
}

(8) 리스트 출력 연산

void print_list(char* msg)
{
    Node* p;
    printf("%s[%2d]: ", msg, size());
    for (p = get_head() ; p!=NULL ; p=p->next)
        printf("%2d", p->data);
    print("\n");
}

(9) 삽입 연산

void insert_next(Node* befoere, Node* n)
{
    if(n != NULL){
        n->prev = before;
        n->next = before -> next;
        if(before -> next != NULL)
            before->next->prev = n;
        before->next = n;
    }
}

void insert(int pos, int val)
{
    Node* new_node, * prev;
    prev = get_entry(pos - 1);
    if(prev != NULL){
        new_node = (Node*)malloc(sizeof(Node));
        new_node->prev = NULL;
        new_node->data = val;
        new_node->next = NULL;
        insert_next(prev, new_node);
    }
}

(10) 삭제 연산

void remove_curr(Node* n)
{
	if (n->prev != NULL)
		n->prev->next = n->next;
	if (n->next != NULL)
		n->next->prev = n->prev;
}

void delete(int pos)
{
    Node* n = get_entry(pos);
    if(n!=NULL)
        remove_curr(n);
}

(11) 전체 노드의 데이터 합(forward, backward)

int sum_forward() {
	int sum = 0;
	Node* p;

	for (p = get_head(); p != NULL; p = p->next)
		sum += p->data;
	return sum;
}

int sum_backward() {
	int sum = 0;
	Node* p;

	for(p = get_head()->prev; p != get_head(); p = p->prev) {
		sum += p->data;
	}
	return sum;
}

3- 3 리눅스 커널과 연결 리스트

1. 리눅스 커널

: 리눅스 커널에서는 자료형을 구현할 때 연결리스트 형으로 자주 사용하는 편임.

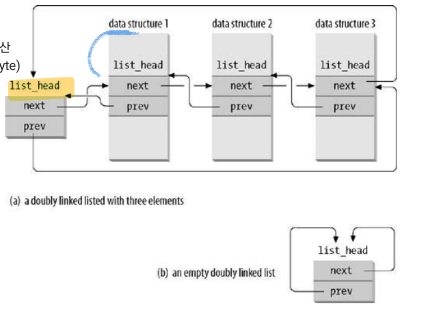
2. 사용법

struct LIST_HEAD_T:
- LIST_HEAD_T 구조체는 이중 연결 리스트의 각 요소를 나타내는 구조체. 이 구조체에는 next와 prev라는 두 개의 포인터 필드가 있으며, 다음과 이전 요소를 가리키는 역할을 함.
init_list_head(struct LIST_HEAD_T *list):
- init_list_head 함수는 주어진 리스트(list)를 초기화하는 함수.
list_del(struct LIST_HEAD_T *entry):
- list_del 함수는 주어진 요소(entry)를 리스트에서 제거.
list_add(struct LIST_HEAD_T *new, struct LIST_HEAD_T *head):
- list_add 함수는 새로운 요소(new)를 주어진 리스트(head)의 처음에 추가.
int list_empty(struct LIST_HEAD_T *head):
- list_empty 함수는 주어진 리스트(head)가 비어 있는지를 확인하는 함수.
list_for_each(pos, head) 매크로:
- list_for_each 매크로는 주어진 리스트(head)를 순회하며 각 요소에 접근하는 반복문을 생성. pos는 현재 순회 중인 요소를 가리키며, 리스트의 끝까지 이동하면 반복문이 종료됨.
list_for_each_safe(pos, n, head) 매크로:
- list_for_each_safe 매크로는 list_for_each와 유사하지만 루프 내에서 요소를 삭제할 때 안전하게 처리할 수 있는 추가 포인터 n을 제공. 이를 통해 요소를 삭제하면서 루프를 반복할 때 문제가 발생하지 않도록 .

_WIN32 환경 매크로:
- _WIN32 환경에서 사용되는 CONTAINING_RECORD 매크로는 다음과 같이 동작함.:
  - CONTAINING_RECORD(address, type, field)는 address가 가리키는 구조체 내에서 type에 해당하는 데이터 구조체의 포인터를 찾음.
  - 이를 위해 구조체 type 내에서 field 멤버의 오프셋을 뺀 결과로 포인터를 계산.
  - address는 찾고자 하는 구조체 내의 field 멤버를 가리키는 포인터이며, 이를 사용하여 type에 해당하는 데이터 구조체를 찾.
그 외 환경 매크로:
- 그 외의 환경에서 사용되는 container_of 매크로는 다음과 같이 동작합니다:
  - container_of(ptr, type, member)는 ptr이 가리키는 구조체 내에서 type에 해당하는 데이터 구조체의 포인터를 찾습니다.
  - 이를 위해 type 내에서 member 멤버의 오프셋을 뺀 결과로 포인터를 계산합니다.
  - ptr은 찾고자 하는 구조체 내의 member 멤버를 가리키는 포인터이며, 이를 사용하여 type에 해당하는 데이터 구조체를 찾습니다.
list_entry 매크로:
- list_entry 매크로는 주로 이중 연결 리스트에서 노드의 데이터 구조체를 검색하는 데 사용됩니다.
- _WIN32 환경에서는 CONTAINING_RECORD 매크로를 사용하여 동작하며, 그 외 환경에서는 container_of 매크로를 사용하여 동작합니다.
- 이 매크로를 사용하면 리스트의 노드 주소로부터 해당 노드의 데이터 구조체 주소를 효과적으로 찾을 수 있습니다.

'Computer Science > Data Structure' 카테고리의 다른 글

[자료구조] 8장 BST (0)	2023.12.16
[자료구조] 4장 스택 (0)	2023.10.16
[자료구조] 2장 자료구조 소개 (0)	2023.10.15
[자료구조] 1장 C언어 리뷰 (2) (0)	2023.09.10
[자료구조] 1장 C언어 리뷰 (1) (0)	2023.09.10

일	월	화	수	목	금	토
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

나는 나은

[자료구조] 3장 Linked List

3-1 리스트

3-2 리스트의 구현

3- 3 리눅스 커널과 연결 리스트

'Computer Science > Data Structure' 카테고리의 다른 글

티스토리툴바

[자료구조] 3장 Linked List

3-1 리스트

3-2 리스트의 구현

3- 3 리눅스 커널과 연결 리스트

'Computer Science > Data Structure' 카테고리의 다른 글

관련글

티스토리툴바