0. Deep neural networks
: 히든 레이어 수가 1개 이상이다. shallow network보다 선형 공간이 더 많다.
4-1. Composing neural networks
1. 1차원 입출력 신경망을 합성하는 경우
: 히든 레이어 2개. 각각의 히든 레이어는 3개의 노드를 가짐. 입출력은 하나


ㄹa) 첫번째 네트워크의 출력 y는 두번째 네트워크의 입력임.
b) 첫번째 네트워크에서는 입력 x를 y로 매핑함. 세 개의 선형 영역으로 이루어짐.
여러 입력 x(회색 원)가 동일한 출력 y(청록색 원)에 매핑 됨.
c) 두번째 네트워크는 y를 받아 y'를 반환하는 세 개의 선형 영역으로 이루어짐.
청록색 원이 갈색 원에 매핑 됨.
d) (c)에서 정의된 두 번째 네트워크의 함수가 세번 복제 됨. 이때 (b)의 기울기에 따라변형됨.
→ 9개의 선형 영역이 생성됨.
2. 2차원 입력을 가진 신경망을 합성하는 경우

a) 첫번째 네트워크의 출력 y는 두번째 네트워크의 입력임.
b) 첫번째 네트워크에서 입력이 2개, 히든 레이어의 노드 수가 3개이므로, 입력 차원은 2차원이고, joint는 3개
c) 두번째 네트워크에서 입력이 1개, 히든 레이어의 노드 수가 2개이므로, 입력 차원은 1차원이고, joint는 2개..이어야하는데 왜 1개냠,,@@
d) 첫번째 네트워크에서 나오는6개의 nonflat regeions은 두번째 네트워크에 의해서 영역이 2배 되어 13개의 linear-regions를 갖게 됨.
3. 입력 공간을 접는 deep network

a) 첫번째 네트워크의 입력 공간을 접음(fold).
b) 두번째 네트워크는 이 접힌 공간에 자신의 함수 적용.
c) 다시 펼쳐(unfolding) 최종 출력을 나타냄.
4-2. From composing networks to deep networks
1.네트워크 합성 → deep network
: 지금까지 두개의 shallow network의 합성으로 보았다면 이번엔 하나의 deep network로 보자.






4-3 Deep neural networks
1.(4-2)에서 만든 하나의 deep neural network 레이어별 계산 정리



2. (4-2)에서 만든 하나의 deep neural network 출력 그래프
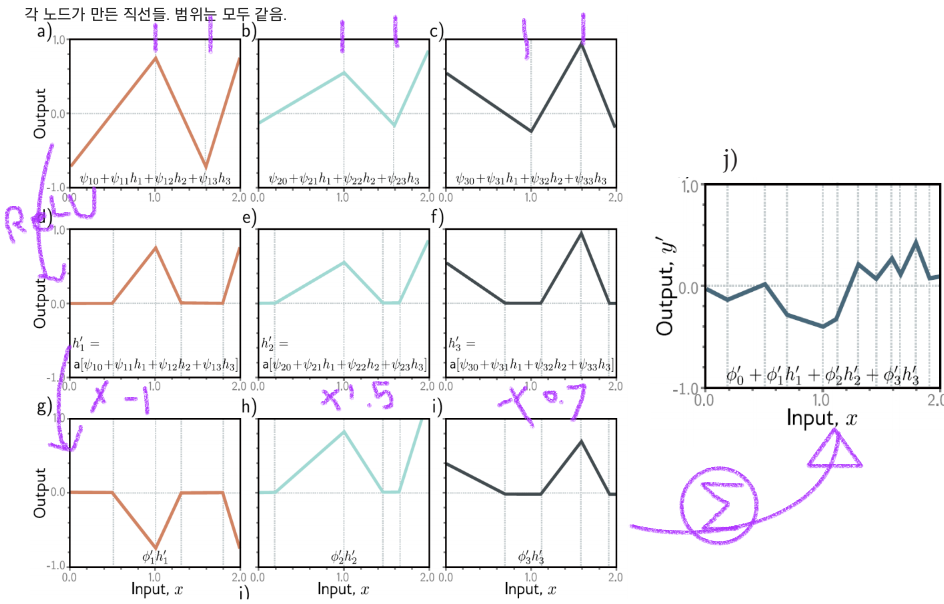
a-c) 두번째 히든 레이어의 입력: 3개의 분할 선형 함수로 만들어짐.
d-f) 각 분할 선형 함수는 ReLU로 clipping됨.
g-i) 각 가중치 ϕ'1, ϕ'2 및 ϕ'3를 곱해줌.
j) ϕ’0와 g,h,i를 더해줌.
3. Hyperparameters
:모델 파라미터를 학습하기 전에 선택해야 하는 것.
1) 너비(width): 히든 노드의 개수
2) 깊이(depth): 히든 레이어의 개수
: 히든 레이어의 총 노드 수는 네트워크 성능(capacity) 측정 척도이다.
: width와 depth가 많아지면 오차는 줄어듦.
: 레이어 수를 K개 라고 할 때, 각 레이어에 있는 노드의 수를 D1, D2, ... DK라고 하겠다.
4-4 Matrix notation
1. deep neural netwok에서 행렬 표기법.
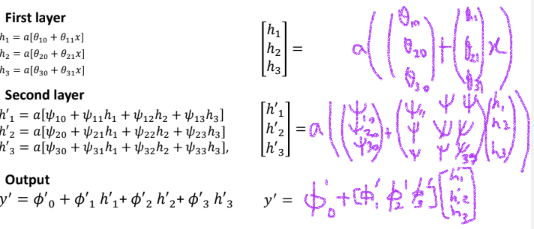
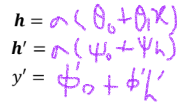
2. deep neural network에서 행렬 표기법의 예
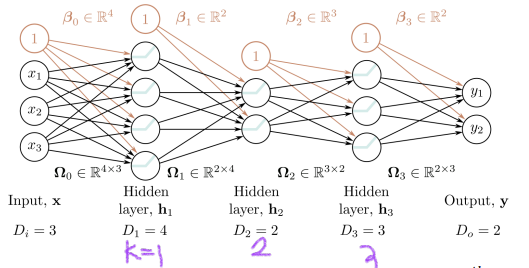
- 가중치는 Ωk 행렬에 저장됨. 이 행렬은 이전 레이어의 활성화를, 선행 레이어의 사전 활성화(pre-activation)로 만들기 위해 곱셈됨.
- 바이어스는 벡터 βk에 저장됨.
3. 벡터들 일반화.
▪ ℎ𝑘: 레이어 𝑘의 히든노드들
▪ 𝛽𝑘: 레이어 𝑘 + 1에 기여하는 바이어스들
▪ Ω𝑘: 레이어 𝑘에 적용되고 레이어 𝑘 + 1에 기여하는 가중치들
→ 𝒉1 = 𝑎[𝜷0 + 𝜴0𝒙], 𝒉2 = 𝑎[𝜷1 + 𝜴1𝒉1], 𝒉3 = 𝑎[𝜷2 + 𝜴𝟐𝒉𝟐], …
𝒉k = 𝑎[𝜷k-1 + 𝜴k-1𝒉k-1]
→ 𝒚 = 𝛽k + Ωkℎk
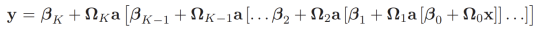
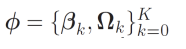
4-5 Shallow vs. deep neural networks
1. 선형 영역 개수와 파라미터 수의 비교
| Shallow network (노드 수: input1, output1, hidden 2이상) |
Deep neural network (노드 수: input1, output1, hidden 2이상) |
|
| 선형 영역 수 (linear regions) | D + 1 | (D + 1)^K |
| 파라미터 수 | 3D + 1 * 가중치: 2D개 * 바이어스: D + 1개 |
3D + 1 + (K - 1)D(D + 1) (fully connected 한정) |
2. 선형 영역의 수
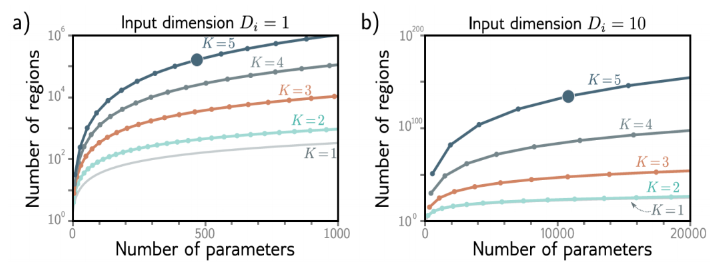
a) 인풋 노드가 1개일 때 b) 인풋 노드가 2개일 때
3. 깊이 효율성(Depth efficiency)
:shallow와 deep 모두 임의의 함수를 근사화 할 수 있지만, deep이 더 효율적임. shallow는 기하급수적으로 더 많은 히든 레이어의 노드를 필요로 함.
→ depth efficiency!!
4. 크고, 구조화된 입력
: 지금까지는 fully connected를 봤지만 이는 이미지같은 입력에는 실용적이지 않음.
→ Convolution 사용!! (local global processingd으로 합성하여 사용!)
5. 훈련 및 일반화
: deep은 shallow보다 쉽게 학습. → 그러나 깊이가 커지면 어려워짐. → Residual Networks를 사용하자!
: deep은 shallow보다 쉽게 일반화.
▶ Deep neural network는 2개 이상의 hidden layer를 가지고 있다.
▶ 첫번째 네트워크는 fold 역할을 하고, 두번째 네트워크는 piecewis linear fumction을 적용
▶ Hyperparameters: hdden 레이어 층의 개수, hidden layer의 노드 개수
▶ Shallow network보다 deep network가 함수 근사화에 효율적임!
'Computer Science > Artificial Intelligence' 카테고리의 다른 글
| [인공지능] SP06. Fitting Models (0) | 2023.11.08 |
|---|---|
| [인공지능] SP05. Loss functions (0) | 2023.10.21 |
| [인공지능] SP03. Shallow neural networks (0) | 2023.10.18 |
| [인공지능] 6장/ 7장/ 8장 (2) | 2023.10.17 |
| [인공지능] 5장 Training Multi-layer preceptron (0) | 2023.10.01 |



