7.1 클러스터링 개요
클러스터링 - 비슷한 것끼리 묶는 것.
데이터가 쌓였을 때 가장 쉽게 할 수 있는 데이터 분석법.
좋은 클러스터링?
내부에서는 가깝고, 클러스터 간은 멀어야 좋음.
The Curse of Dimensionality(차원의 저주)
대부분 엄청 많은 차원을 사용함.
근데 차원이 높아지면 점들 간의 거리가 비슷해짐.
클러스터링 예시
- SkyCat: 하늘의 천체들을 비슷한 애들끼리 묶음
- 음반 클러스터링: CD를 산 사람들로 CD를 표현함.
- 문서 클러스터링: 문서를 이루는 단어로 문서를 표현함
- DNA 서열 클러스터링: DNA 서열 간의 편집 거리를 이용해 클러스터링
→ 뭔가 distance를 구할 수 있는 방법만 있으면 clustering할 수 있다!
vector similarity → cosine distance
set similarity → Jaccard distance
points similarity → Euclidean distance
클러스터링 방법
- 계층적 클러스터링: 초기에는 각 점이 클러스터고, 지날 수록 가까운 클러스터 2개가 하나가 됨.
- Point Assignment: 데이터 포인트를 이미 있던 클러스터의 적절한 자리에 넣는 것.
7.2 계층적 클러스터링
계층적 클러스터링: 초기에는 각 점이 클러스터고, 지날 수록 가까운 클러스터 2개가 하나가 됨.
계층적 클러스터링의 고민 2가지
- 가까운 정도를 어떻게 정의하냐!
- 클러스터를 어떻게 표현할 것이냐!
Euclidean case에서는
centroid는 points의 평균.
centroid로 각 클러스터의 위치를 나타내어, 다른 클러스터 간의 거리를 나타냄.

Non-Euclidean case에서는 평균의 개념이 없음!
아래의 3가지 접근 방법을 사용.
(1) clustroid
: 클러스터 안에서 다른 점들과 가장 가까운 point, centroid와 개념은 비슷함.
hmm.. 가장 가까운 point ?
- 제일 먼 애들까지의 거리가 가장 작은 point
- 다른 애들과의 평균거리가 가장 작은 point
- 다른 애들과의 거리를 제곱하고 합했을 때 가장 작은 point
(2) intercluster distance
- 서로 다른 클러스터에서 나온 낱낱의 점들 중 가장 작은 거리
(3) cohesion(응집력)
- 클러스터 안에서 가장 먼 두 점의 거리(지름)로 판단
- 클러스터 안의 점들 사이의 평균 거리로 판단
- 밀도로 판단. (ex. 지름/점의개수)
7.3 k-means 알고리즘
유클라디안 공간을 가정한다!
과정
서로 다른 클러스터에 속할 가능성이 높은 k개의 점들을 선택해 센트로이드로 만듦;
FOR 남아 있는 각 점 p에 대해 DO
p에서 가장 가까운 센트로이드를 찾기;
p를 그 센트로이드의 클러스터에 추가;
p를 반영해 그 클러스터의 센트로이드를 조정;
END
그러면 k는 어떻게 정하지?
k가 너무 작으면 센트로이드로 부터 다른 점들 사이의 거리가 매우 길어짐.
k가 너무 크면 클러스터 내 평균 거리가 유의미하게 향상되지 않음.

k가 같으면 항상 클러스터링 결과는 같다? -> false
: 초기값이 랜덤하기때문.
BFR Algorithm(Breadley-Fayyad-Reina)
k-means 알고리즘의 변형으로, 고차원의 유클리드 공간에서 클러스터링 하려고 만듦.
가정: 클러스터는 보통 센트로이드 중심으로 분포해야 함
포인트들을 세가지로 나눔.
- Discard set(DS): 센트로이드랑 충분히 가까워서 무시.
- Compression set(CS): 누구랑도 크게 안가까운데 자기들끼리 오글오글 모여있는 애들
- Retained set(RS): 고립된 포인트들
센트로이드와 클러스터를 주기적으로 업데이트 해줘야 하므로
discard set을 완전히 지우는 것이 아니라 summarizing해서 가지고 있어야 함.
요약 방법 3가지 - DS와 CS는 아래의 정보를 가지고 있음.
- 점의 수 N
- 각 차원에서 점 좌표의 합을 나타내는 벡터 SUM
- 각 차원에서좌표의 제곱의 합을 나타내는 벡터 SUMSQ
차원 수가 d라고 할 때 각 클러스터의 크기는 2d+1로 표현됨.
(dimension만큼의 sum과 sumsq와 1개의 n)
-> 분산은 (SUMSQ/N) - (SUM/N)^2로 나타냄
BFR Algorithm의 데이터 처리
- 충분히 가까운 애들은 DS에 넣고, N과 SUM, SUMSQ를 업데이트한다
- 메인메모리와 클러스터링을 사용하여 겉도는 애들은 RS로, 좀 모여있는 애들은 CS에 넣는다
- 새로 만들어진 CS는 기존의 CS와 합칠 건지 고려한다
- 위의 1,2,3을 반복하고 마지막 라운드의 경우, 가까운 CS는 합치고, 모든 RS 포인트는 가까운 클러스터에 넣버린다.
고려1: 새로운 점을 클러스터에 넣을 때 - 2가지 접근
- 현재 가까운 센트로이드에 속한 점들에 높은 확률을 부여.
- Mahalanobis distance

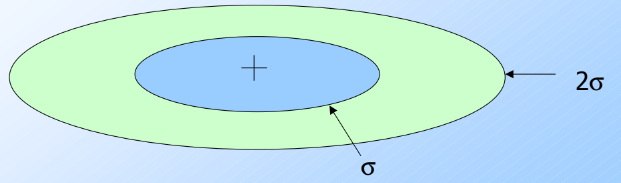
해당 점과 centroid간의 mahalanobis 거리가최소가 되는 culster를 고르고, 그 값이 threshold보다 작은 경우 그 클러스터에 넣음.
고려2: 두 클러스터 합치기
두 클러스터의 분산을 구해 그 분산이 threshold보다 작으면 합침.
N, SUM, SUMSQ를 가직고 있어서 분산 구하기 쉬움.
7.4 CURE 알고리즘
앞서 본 BFR이나 k-means알고리즘은 잘 분포되어있다고 가정하이고, outlier를 잘 판단 못함.
세상에는 다양한 분포로 생긴 애들이 있음.~
이를 해결하기 위해 CURE가 나옴.
CURE 알고리즘 과정
- 메인 메모리 용량만큼 sample point를 뽑음.
- 초기 클러스터를 만들려고, 계층 클러스터링을 진행.
- 각 클러스터에서 최대한 멀리 떨어져 있는 점들로 대표점을 뽑음. (대표점은 여러 개일 수도)
- 이 대표점들을 해당 클러스터의 centroid 방향으로 20% 정도 수축시킴.
- 마지막에 남은 점들은 가장 가까운 클러스터에 포함시켜버림.
Reference
https://minutemaid.tistory.com/83
BFR Algorithm
BFR Algorithm (Bradley-Fayyad-Reina) K-means의 경우 데이터 집합이 메모리에 올라갈 수 있는 사이즈일 때만 사용 가능하기 때문에, BFR알고리즘은 K-means를 변형하여 매우 큰 데이터 집합을 다룰 수 있게 한
minutemaid.tistory.com
'Computer Science > Web Information System' 카테고리의 다른 글
| [웹정보] ch09 Recomeder Systems 2 (0) | 2024.06.13 |
|---|---|
| [웹정보] ch11. dimensionality reduction (0) | 2024.06.13 |
| [웹정보] ch09 Recomeder Systems 1 (0) | 2024.06.10 |
| [웹정보] ch06 Association Rules2 (0) | 2024.04.20 |
| [웹정보] ch06 Association Rules1 (0) | 2024.04.20 |



