11.0 Intro
하나의 행렬은 2개의 행렬의 곱으로 근사화할 수 있음!
sparse한 하나의 행렬을 꽉 찬 2개의 행렬의 곱으로 근사화 한다면?
→ 실제 행렬이 예측 못한 rating을 잘 예측할 수 있지 않을까!
이게 가능한 이유! → latent factor!
11.1 UV Decomposition

❓r은 어떻게 정하지❓
r이 hidden factor의 수일 때 결과가 잘 나온다
ex. r이 장르의 개수일 때 good
m: 사람 x 영화, u: 사람 x 장르, v: 장르 x 영화
❓Error 측정은 어떻게 하지❓
분해가 잘 되냐 안되냐 판단하는 기준: RMSE(Root-Mean-Square-Error)


❓U와 V는 어떻게 찾아내지❓
step1) latent factor의 개수인 r을 구한다.
step2) U와 V를 Error가 낮아지는 방향으로 업데이트한다.
(이때 unknown rating인 것은 Error 계산할 때 빼라!)
❓local minima에 어떻게 안빠지지❓
- Use many different starting points
- Simulated annealing: 겅중겅중 다니다가 local minima에서 빠져나오고, global minima로..
11.2 Singular-Value Decomposition
SVD란!
n*m의 행렬을 n*r, r*r, r*m 세가지 행렬로 나누는 것
(1) Rank of a Matrix
Rank? 독립적인 행의 최대 개수
ex. Rank가 2이면, 독립적인 두 행이 존재., 어떤 세 행도 독립적이지 않음.
그러면 독립적인게 뭐야? → 선형 결합으로 표현될 수 없다는 의미


중요한 사실!
: 어떤 행렬의 rank가 r이라면, 이는 공통 차원이 r인 행렬로 분해할 수 있음.
(2) Orthonormal Bases (직교 정규 기저)
- orthogonal: 두 벡터의 곱이 0이라는것.
- unit vector: 길이가 1인 벡터. (길이는 각 요소를 제곱해서 더하는 것)
- orthonormal bases는 두 벡터가 직교하는 단위 벡터의 집합.

SVD에서 U와 V는 column-orthonormal함. (VT는 row-orthonormal)
(3) SVD에 대해 더 자세히!
- 특이값(singular value): Σ의 대각성분
- 랭크가 r이면 정확히 분해하는 것이 항상 가능하지만
- 보통 r을 랭크보다 훨씬 작게 만들고 싶어해서 가장 작은 특이값들을 0으로 설정함.

예시를 들어서 설명해보겠다.
위의 행렬은 user-movie 행렬이다.
위에는 user와 movie만 나와있지만, 사실 영화마다 장르라는 "latent factor"가 있다.

예시에서는 SciFi와 Romance만 고려한다. 위의 행렬을 SVD분해하면

- U: user - concept
- Σ: strength of concept, sorting되어있음.
- V: movie - concept
(4) Lowering the Dimension
앞서 말했듯이 작은 특이값을 0으로 만들자!
어차피 개개인의 평점을 하나하나 신경쓰는게 아니라 경향성을 일반화하는 것임.


❓잘 근사했는지 어떻게 측정하지❓
Frobenius norm
: 행렬의 모든 원소의 제곱의 합의 제곱근 = RMSE
작은 특이값들을 0으로 만들어 r을 최소화하면 오차가 작아짐.
❓그러면 좋은 r은 뭐지❓
특이값 집합의 에너지 = 특이값 제곱의 합
남겨진 특이값의 에너지가 적어도 90%는 가지도록 선택!!

+) Finding Eigenpair
<Eigen vector x 구하기>

위의 과정을 변화가 거의 없을 때까지 반복함.
<Eigen value구하기 λ >

(5) How to Compute the SVD



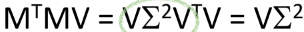

즉!! V는 MTM의 eigen vector이다!
따라서 MTM의 eigen vector를 구하고 나면 V를 구하게 되는 것이고,
그걸 가지고 eigen value인 Σ^2을 구할 수 있을 것이다!!
'Computer Science > Web Information System' 카테고리의 다른 글
| [웹정보] ch09 Recomeder Systems 2 (0) | 2024.06.13 |
|---|---|
| [웹정보] ch07 Clustering (0) | 2024.06.11 |
| [웹정보] ch09 Recomeder Systems 1 (0) | 2024.06.10 |
| [웹정보] ch06 Association Rules2 (0) | 2024.04.20 |
| [웹정보] ch06 Association Rules1 (0) | 2024.04.20 |



