3-1 부호있는 네트워크와 구조적 밸런스 이론
1. Signed Networks
: 양, 음의 관계를 가진 네트워크. 기본 단위는 부호있는 삼각형. 아래와 같이 directed, undirected로 나타 낼 수 있음.
- 양의 관계: friendship, trust, positive sentiment, …
- 음의 관계: enemy, distrust, negative sentiment, …

2. Theory of Structural Balance(구조적 밸런스 이론)
- balanced: 내 친구의 친구는 친구이다. 적의 적도 친구이다. 적의 친구는 나의 적이다.
→ 음(-)의 개수가 짝수, 양의 개수가(+) 홀수면, balance !
- unbalanced: 나의 친구의칙구가 나와 음의 관계임.
→ unbalanced한 그래프를 하나라도 포함하면 전체 그래프도 unbalanced.


3. Local Balance → Global Faction(파벌)
: Balance는 global coalition(전역적인 연합)을 의미한다.
- 만약 모든 삼각형이 balanced 하다면 아래의 두 경우로 나타난다.


4. Global Faction의 예시
(1) 1971년 파키스탄으로부터 방글라데시의 독립 문제로 미국이 파키스탄을 지원하는지 예측.

(2) 1차 세계대전의 발발 배경






3-2 일반적인 네트워크에서의 균형
1. complete graph의 필요충분조건
- Local view: 균형 잡기 위해 없는 edge를 채우는 것
- Global view: 그래프를 두 개의 연합으로 나누는 것
2. Signed 균형 네트워크인지 확인하는 방법
: 그래프가 balanced 상태이려면 반드시 음의 관계(-)를 홀수개 가져야하고, 어떤 사이클도 존재하지 않아야한다!
- 양의 관계(+)를 가진 connected components 찾는다
- 각 componentㅇ에 대한 슈퍼 노드 생성한다
- 슈퍼 노드의 멤버 사이에 음의 관계(-)가 있다면 2개의 component로 연결한다. 그러면 2개의 component가 각각의슈퍼 노드가 된다.
- 슈퍼노드를 BFS를 이용해 편을 나눈다.
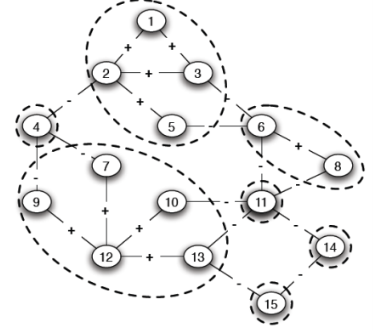
각 노드가 슈퍼노드가 되었지만 C와 D는 같은 Left이므로 Unbalanced하다. 따라서 둘 사이의 edge를 제거해야한다.
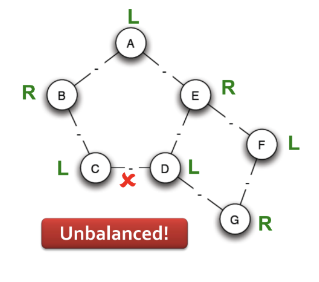
3-3 실제 데이터 탐색
1. Real Large Signed Networks
- Epinions: 제품 리뷰 신뢰/ 불신
- Wikipedia: 위키피디아 관리자가 되는 것을 지지/ 반대
- Slashdot: 댓글 좋아요/적
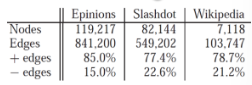
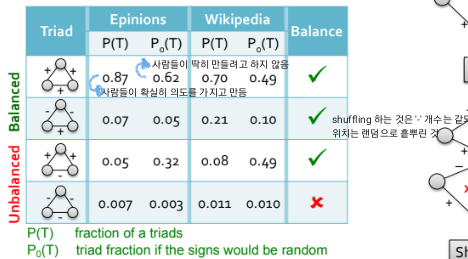
2. Network data에서의 균형
- P(T): 실제 데이터
- P0(T): 섞인 데이터('-'의 개수는 같되, 위치는 랜덤으로 흩뿌린 것.)
: 세번째와 같이 이론적으로는 unbalaced한 데이터의 조합도 있었다.
3. Signed network의 전체적인 구조
- Embeddedness of link (A,B): 얼마나 커뮤니티 내에 쏙 들어가 있나를 수치화. 공유하는 이웃의 수가 높을 수록 큼.
- positive ties가 더 embedded된 경향이 있다.(더 엉켜있고, 뭉쳐있다.)
- 위키피디아에서 투표의 공개는 이러한 embeddedness를 약화시킨다.
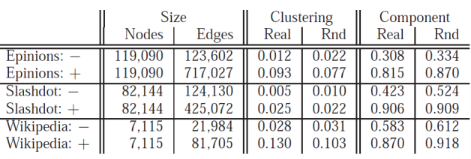
- +/- net 모두 실제 max Component는 기준(random)보다 작음.
- + net은 Clustering 기준보다 더 뭉쳐 있음.
- - net은 Clustering 기준보다 더 덜 뭉쳐 있음.
3-4 Status (지위)
1. Status
: 사람들은 보통 링크의 방향을 무시해 균형을 적용해 옴. → Status를 고려하자!
- A + → B: B가 더 높은 지위
- B - → A: B가 더 낮은 지위.
이를 사용하면 A - → B를 A ←+B로 나타낼수 있음!
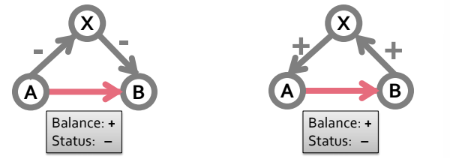
2. Status vs. Balance
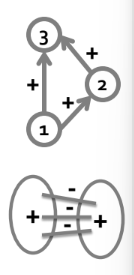
- Status → 계급: 모든 링크의 부호가 '+'이면 사이클을 가져서는 안됨!
- Balance → 연합: 방향을 무시하고, 이분 그래프이어야 함.
3. Status에 관한 이론
▶ 우리는 A와 B 사이의 관계를 위해서 X와의관계도 함께 생각해주어야 하는가? 아닌가?
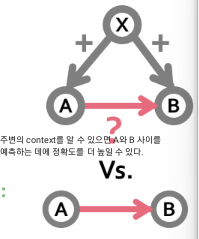
<<고려해야할 점>>
1) 링크는 삼각형 내에 포함됨: 이 삼각형은 부호에 대한 맥락을 제공.
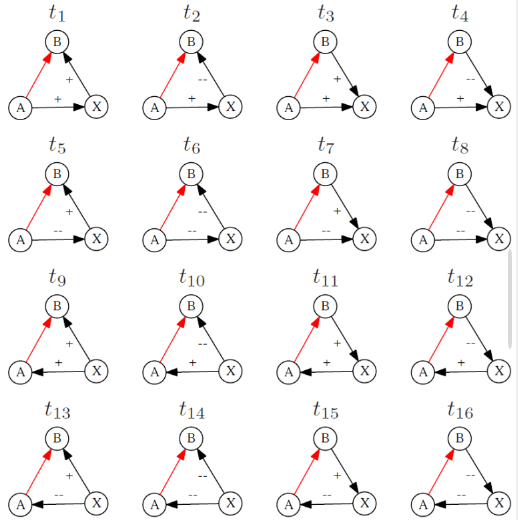
2) 사람들마다다양하게 나타난다!

'Computer Science > Software Application' 카테고리의 다른 글
| [소응] 15장 Sponsored Search Markets (0) | 2023.12.15 |
|---|---|
| [소응] 10장 Matching Markets (0) | 2023.12.15 |
| [소응] 9장 Auctions(경매) (0) | 2023.12.15 |
| [소응] 2장 네트워크의 커뮤니티 구조 (0) | 2023.09.23 |
| [소응] 1장 웹 그래프(Web Graph) (0) | 2023.09.13 |


