15-1 Advertising Tied to Search Behavior(검색 행동에 연결된 광고)
1. Paying per click
- 검색엔진이 어떻게 클릭당 가격을 설정할까?
- 이거 어려운 일!: 키워드 조합이 너무 많고, 수요가 변해 합리적인 가격을 유지하기 어려움..
- 대신! 검색 엔진은 경매를 사용해 가격을 결정!
- 하나의 슬롯: sealed-bid second-price auction
- 여러 광고 슬롯이 다른 가치를 갖는 경우: 복잡해!
2. Designing an Auction
- 검색 엔진이 광고주의 클릭에 대한 가치를 알면 - slot과 advertiser간의 매칭
- 검색 엔진이 광고주의 가치를 모른다면 - truth bidding을 이끌어내거나 그냥 untruthful bidding 처리
- VCG mechanism은 가치를 모르는 상황에 대한 해결법. 하지만 사실 GSP(Generalized Second-Prices Auction)를 더 많이 씀. 그 이유는 기대 수익이 더 높을 것이라고 예상함.
15-2 Advertising as a Matching Market
1. Clickthrough Rates and Revenues Per Click
- 각 슬롯은 고유의 clickthrough rate을 가지고 있음
- 시간 당 얼마나 클릭 되나
- 각 광고주는 revenue per click을 가지고 있음
- 클릭 당 기대 수익
2. Constructing a Matching Market for Particular Keyword
위의 문제를 matching market 문제로 바꾸자!
기본 개념들
- ri: 슬롯 i의 클릭률
- vj: 슬롯 광고주 j의 클릭당 수익
- ri*vj: 광고주 j가 슬롯 i에 표시될 때 받는 혜택
- 광고주가 더 많으면?
- 클릭율이 0인 추가 가상 슬롯을 생성하자!
- 슬롯이 더 많으면?
- 모든 슬롯에 대해 가치가 0인 추가 광고주를 생성하자!
3. Obtaining Market-Clearing Prices
- 10장에서 모든 matching market에서는 MCP가 존재한다는 것을 보았음.
- 이를 광고 시장에 적용
- 광고주들은 서로 다른 슬롯 선호
- 광고주를 슬롯에 할당한 결과는 총 가치를 최대화,
- Valuation = 클릭율 * 클릭당 수익
- 위의 값을 최대화하려면 가장 높은 클릭율을 가진 슬롯을 클릭당 수익이 최대인 광고주에게 제공.
- 이는 광고주의 가치를 실제로 알 경우에만 수행 가능.
- 그러면 알 수 없는 없는 경우는 어떡하쥥~
- 광고주에게 가치를 신고하도록 의존...
- 해결법? -> 다음장에서
15-3 Encouraging Truthful Bidding in Matching Mar- kets: The VCG Principle
- 초기에는 first-price auction을 사용했고, 광고주들이 진실했음
- 하지만 시간이 지날 수록 경쟁자를 따돌릴려고 truth valuation으로 bidding하지 않음.
- 결과적으로 난장판됨.
- 단일 품목 auction의 경우 second-price auction을 선택.
1. The VCG Principle - Vickrey-Clarke-Groves
진실된 가치 보고를 촉진하기 위한 원칙.
각 참가자가 경매의 결과에 미치는 영향에 따라 지불할 가격을 결정.
- matching 시장에는 많은 항목이 존재해 second-price auction은 어려움.
- auction의 승자는 아이템을 받음으로써 다른 입찰자들에게 일으키는 harm만큼 지불.
- 이는 자신의 입찰이 다른사람들에게 미치는 영향을 미치는 것을 앎,
- 이는 더 진실된 보고를 장려하는 것으로 나타남.

x가 존재하지 않았다면 y와 z에게 할당된 아이템에 대한 가치가 각각 10만큼, 3만큼 개선됨.
10+3=13은 x가 지불해야하는 가격임.

→ 이러한 방식으로 slot의 가격을 책정함.
- S를 판매자 집합, B를 구매자 집합이라고 하자.
- 아이템 i를 판매자 j에게 주면, 나머지 구매자가 얻을 수 있는 최고 총가치는 V_S-i_B-j
- 구매자 j가 존재하지 않지만 아이템 i가 여전히 남아있을 때 얻을 수 있는 최고 총가치 V_S_B-j
- 아이템 i에 대한 가격은 아래와 같다. 그리고 이 값은 harm의 양과 같다.

2. VCG price-setting 과정
- 구매자에게 validation을 발표하도록 요청
- 아이템을 구매자들에게 할당
- VCG가격 부과
→ 이는 진실을 말하는 것이 우세하게 하는 전략임.
3. VCG vs market-clearing prices
MCP - 게시된 가격(판매자가 가격을 발표하고 이를 동의하는 구매자가 구매.)
VCG - 개인화된 가격(누가 사냐에 따라 다른 가격)
MCP - ascending auction일반화
VCG - second-prices 일반화
15-4 Analyzing the VCG Procedure: Truth-Telling as a Dominant Strategy

- buyer j는 정직한 발표에서 벗어날 이유가 없음.
- 만약 거짓말을 하면 아래의 두 경우가 생김
- 첫째, 거짓말을해도 그녀가 받는 item에는 영향을 안줌 - 이 경우 payoff는 그대로: v_ij - p_ij
- 둘째, 거짓말로 인해 다른 item을 받게되는 경우. 이때는 payoff가 변함: v_hj - p_hj
- 따라서 우리는 거짓말을 치면 안되는 것을 보여줘야해서 아래를 증명해야함
- v_ij - p_ij >= v_hj - p_hj
<<v_ij - p_ij >= v_hj - p_hj 증명!!>>
아까 구한 VCG 식을 대입하면 아래와 같아짐


사실 왼쪽 항은 가능한 perfect matching 중 최대 총 가치를 달성하는 matching이므로
아래와 같이 바꿔 쓸 수 있음.
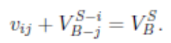
사실 오른쪽 항은 j와 h를 짝지어주는 일치에 대해서만 최대 총 가치를 달성하는 matching이므로
아래와 같이 바꿔 쓸 수 있음
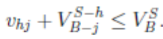
따라서 진실되게 발표하는 것이 VCG에서 유리한 전략임을 증명함!
- 사실 지금까지는 광고주가 얻는 총 가치를 극대화 하는 데에 중점을 둠.
- 하지만 검색 엔진 회사는 사실 수익을 중요하게 생각함.
- 이런 방면에서 VCG는 판매자 수익을 최대화하는 최상의 방법은 아님.
- 다음장에서...
15- 5 The Generalized Second Price Auction
- .검색 엔진 회사들은 GSP를 채택.
1. GSP procedure
- 각 광고주는 클릭당 지불할 가격을 나타내는 숫자 b_j를 발표(v_j와 같을지는 광고주 마음)
- 슬롯 i를 i번째로 높은 입찰자에게 i+1번째로 높은 입찰가에 대한 클릭당 가격으로 수여.

2. VCG vs GSP
단일 슬롯이 있으면 결과가 같지만, 여러 슬롯이 있으면 가격을 생성하는 규칙이 다름.
(1) VCG의 규칙

(2) GSP의 규칙
: i번째로 높은 입찰자가 bi+1의 클릭당 가격으로 슬롯 i를 획득하게 될 것임.
3. Analyzing GSP
: Nash equilibria를 고려해보자. 어떤 광고주도 행동을 변경 안 할 bid 집합을 찾아야한다.
- (-) GSP에서는 진실을 말하는 것이 Nash equilibira를 이루지 않을 수 있음.
- (+) GSP에 대해 항상 Nash equilibria를 만족하는 bid 집합과 항상 광고주의 가치를 극대화하는 것이 있음
4. Truth-telling may not be an equilibrium for GSP
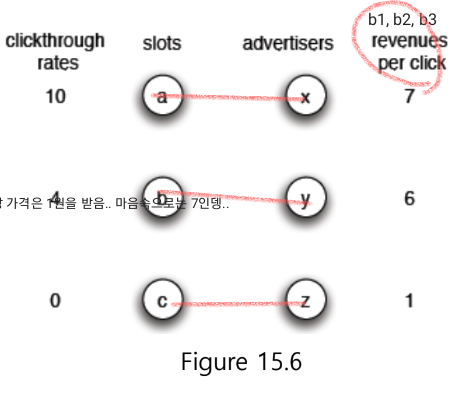
x가 거짓말을 안치면 10*7 - 10*6 = 10만큼의 payoff를,
x가 거짓말을 쳐서 자신의 bid가 5라고 하면,
x는 1의 가격으로 b를 얻을 수 있게 되어, 4*7 - 4*1 = 24만큼의 payoff를 얻을 수 있음.
-> 거짓말쳤을 때 더 많은 payoff..!
5. Multiple and Non-Optimal Equilibria
(1) Equilibrium1
x가 5만큼, y가 4만큼, z가 2만큼 bidding하면 equilibrium 형성.
(x가 4보다 작게 bidding해도 바꿀 이유가 없음.)
(y가 5보다 높게 bidding해도 바꿀 이유가 없음.)
(2) Equilibrium 2
x가 3만큼, y가 5만큼, z가 1만큼 bidding하면 equilibrium 형성.
그러나 cross된 상황이 나오므로 사회적으로 최적은 아님!!
사회적으로 최적이 아닌 equilibrium구조에 대해 잘 안 알려져 있음.
6. The Revenue of GSP and VCG
- GSP로 했을 경우 VCG보다 높거나 낮을 수도 있음.
- 위 장의 경우 48(10*4 + 4*2)이거나 34(3*10 + 4*1)
- VCG라는 예쁜 방법이 있지만 GSP를 하는 이유: 수익때문!!
- VCG로 하면 44 수익을 얻을 수 있음.
'Computer Science > Software Application' 카테고리의 다른 글
| [소응] 10장 Matching Markets (0) | 2023.12.15 |
|---|---|
| [소응] 9장 Auctions(경매) (0) | 2023.12.15 |
| [소응] 3장 부호있는 네트워크 (0) | 2023.10.11 |
| [소응] 2장 네트워크의 커뮤니티 구조 (0) | 2023.09.23 |
| [소응] 1장 웹 그래프(Web Graph) (0) | 2023.09.13 |


