Mining of Massive Datasets
Jure Leskovec Stanford University, Anand Rajaraman Rocketship Ventures, Jeffrey D. Ullman Stanford University
Chapter03 Finding Similar Items
Application: Entity Resolution
Entity Resolution:
두 엔티티가 같은지를 알아내는 것!
같은 값을 가진 상황에서 이들을 merge하고 싶을 때 사용을 많이 함.
Matching Customer Records 문제
A회사가 B회사의 고객리스트에 광고하고 싶어함.
그렇다면 몇 명 치 요금을 내야할까?
A회사 리스트와 B회사의 리스트가 겹치는 것도 있지 않겠냐!
→ LSH로 해결하자!
name, address, phone 중 하나라도 같으면 같은 사람이라고 해보자~
운이 안 좋아서(사용자가 정보를 잘못 입력했다든지~) 같은 사람을 다른 사람이라고 판단할 수 있음.
→ Design measure "score"
LSH가 식별한 쌍에게 점수를 부여함으로써 높은 점수를 가진 pair를 candidate에 넣자!
(+name과 같은 char나 string은 아스키코드로 바꾸는 것이 아닌 정렬을 해)
Application: Similar News Articles
Similar News Articles:
여러 신문사의 웹사이트에 같은 기사가 나타남.
기사 내용은 다 같은데 로고가 다르다든지, 광고가 포함되어있다든지, 조금 잘라낸다든지 조금씩만 다름.
이 문제를 해결하기 위해 minhashing, LSH를 사용하지 않고 Shingling만 이용할 것임!
Specialized Shingling Technique:
광고에는 stop word가 많이 나오지 않는다는 점을 사용해 Shingle을 아래와 같이 정의함.
Shingling: stop word & the next two following words
→ shingling이 광고보다 article에서 더 많이 나오게
Distance Measures
Distance measure가 되기 위한 조건 :

여기서 4번의 triangle inequality는 쉽게 말해, 어디 거쳐가는 것은 바로 가는 것보다 같거나 커야한다는 것이다.
Euclidean Distance:
Lp norm은 다음과 같이 정의 할 수 있다.

따라서 L1-norm과 L2-nrom을 그림으로 나타내면 아래와 같다.

아래 나오는 Cosine distance, Jaccard distance, Edit distance는 non Euclidean distance이다.
Cosine Distance:
for vectors = angle between the vectors(각도가 벌어진 정도)
구하는 방법: 내적을 구하고 길이로 나눈다.


(cosine dist로 불리는 이유는 내적이 ab cos세타이기 때문.)
이는 L2-disance보다 현실적으로 잘 작용함.
Jaccard Distance:
for sets = 1 - (jaccard similarity)
왜 jaccard distance는 distance measure인가!

아마 조건 1, 2, 3번에 대해서는 어렵지 않게 이해할 수 있었을 것이다.
4번 조건인 Triangle Inequality에 대해 알아보자.

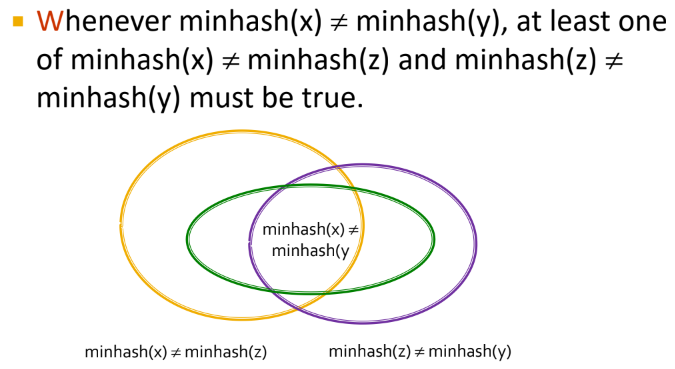
d(x,z)는 minhash(x)와 minhash(z)가 같을 확률을 말한다.
따라서 1 - d(x,z)는 minhash(x)와 minhash(z)가 다를 확률이므로
Triangle inquality 식은 위의 네모 박스 안의 식처럼 수정할 수 있다.
그리고 네모 박스 안의 식은 아래와 같이 증명할 수 있다.
만약 x의 minhashing값과 y의 minhashing값이 다르다면, 아래의 두 가정 중 적어도 하나는 무조건 진실이게 된다.
- x의 minhashing값과 z의 minhashing값이 다르다
- y의 minhashing값과 z의 minhashing값이 다르다
Edit Distance:
for strings = 같게 만들기 위해 insert해야 하는 수와 delete해야 하는 수.
다시말해 한 str을 다른 str로 바꾸려면 얼마나 edit해야 하나!이다
구하는 방법: d(x,y) = |x| + |y| - 2|LCS(x,y)|
다시말해 두 str의 길이 - 2LCS이다.
그럼 LCS가 뭐냐!
longest common subsequence로, 최장 공통 부분 수열이다. 예시는 아래와 같다.

LSH Families of Hash Functions
Definition:
hash function에서 h(x) = h(y)이면 x와 y는 candidate pair가 된다.
LSH family가 무엇이냐! 아래와 같은 형태이다.
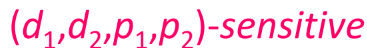
- d1은 거리의 가까움을 표현하는 정도
- d2는 거리가 먼 것을 표현하는 정도
- 만약 d(x,y) <= d1이면, 적어도 p1의 확률로 h(x) = h(y)이다.
- 만약 d(x,y) >= d2이면 최대 p2의 확률로 h(x) = h(y)이다.
위의 정의를 보면 알겠지만 보통 p1이 p2보다 꽤 큰 값을 갖는다.
p1은 1에 가까울 수록 좋고, p2는 0에 가까울 수록 좋다.
만약 hash family H가 (1/3, 3/4, 2/3, 1/4)을 갖는다면 아래와 같이 해석할 수 있다.
- 만약 distance <= 1/3이면, 최소 2/3 이상의 확률로 candidate에 포함됨.
- 만약 distance >= 3/4이면, 최대 1/4 확률로 candidate에 포함됨.
Jaccard similarity, (d1, d2, (1-d1), (1-d2))-sensitive family for any d1 < d2
Amplifying an LSH-Family
앞서 배운 candidate을 찾기 위한 band 테크닉을 기억해보자.
우리는 band 테크닉을 아래처럼 얘기할 수 있다.
- AND -> "rows in band"
- OR -> "many bands"
이게 무슨 소리냐면
AND: 두 밴드가 하나의 candidate이 되기 위해서는 하나의 band안의 모든 row값들이 같아야 한다!
OR: 두 document 중 하나의 row라도 동일하면 candidate이 된다!
라는 의미이다.
① AND of Hash Function -> row 입장!!
r개의 hash function으로 이루어진 family H'는 아래와 같이정의할 수 있다. -> r개의 row!
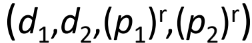
각각의 hash function은 독립사건이므로 r번 곱해서 확률은 p^r 형태이다.
여기서 p1과 p2는 0과 1 사이의수이다.
p2^r은 0에 가까워지므로 좋지만(good),
p1^r은 1에 가까워져야 좋은데 0으로 가까워져서 좋지 않다.(bad)
② OR of Hash Function -> band 입장!!
b개의 밴드로 이루어진 family H'는 아래와 같이 정의 할 수 있다. -> b개의 band!
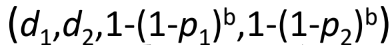
p1의 경우만 살펴 보자면, (1-p1)는 해당 밴드가 같은 bucket에 들어가지 않을 확률이다.
(1-p1)^b는 b번 모두 같은 bucket에 들어가지 않을 확률이다.
1-(1-p1)b는 b번 모두 같은 bucket에 들어갈 확률이다.
p1^r은 1에 가까워지므로 좋지만(good),
p2^r은 0에 가까워져야 좋은데 1로 가까워져서 좋지 않다.(bad)
Combining hash functions:
그러면 AND와 OR를 잘 적절히 섞어야 할 것같은데..!
① AND-OR composition

우선 p^r은 두 밴드 내의 모든 row의 값이 같을 때의 확률이다. 즉, 같은 bucket에 들어갈 확률이다.
그러면 (1-p^r)은 여집합이므로 다른 bucket에 들어가 확률이다.
(1-p^r)^b는 b번 모두 다른 bucket으로 들어갈 확률이다.
그러면 1-(1-p^r)^b는 여집합이므로 b번 모두 같은 bucket으로 들어가 확률이다.

② OR-AND composition
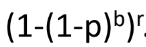

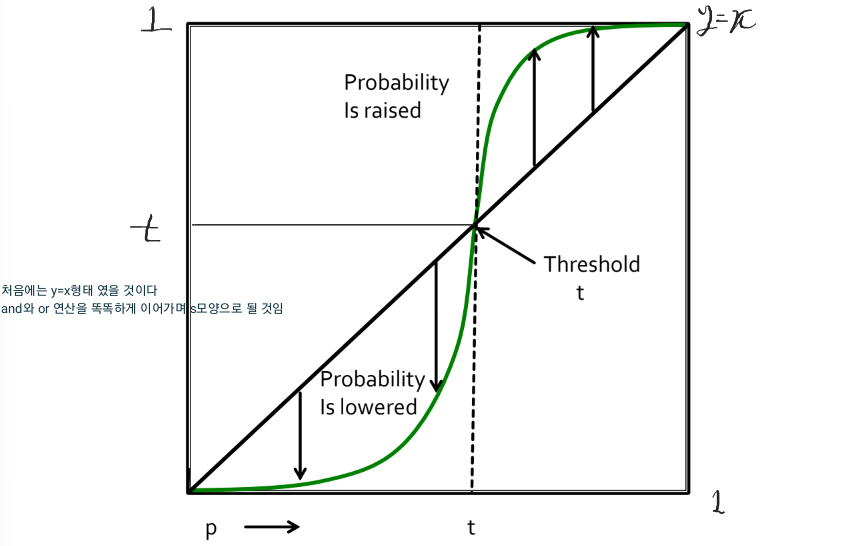
Making steep S-Curves:
이를 그래프로 표현하면 아래처럼되고,
이로서 앞장에서 살펴본 s-curve형태로 된당
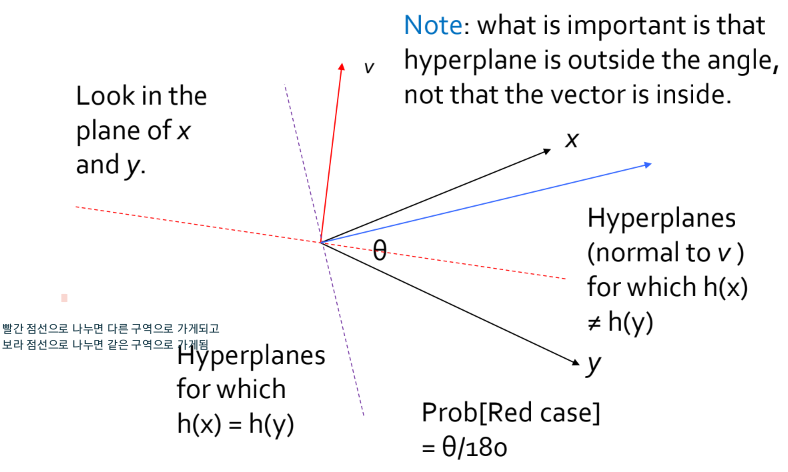
LSH for Cosine Distance
Random Hyperplanes:
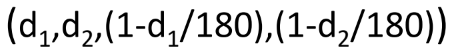
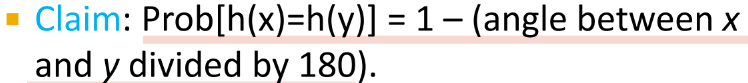
두 별의 각도가 0이면 같은 hyperplane상으로 갈 확률은 1이다.
'Computer Science > Web Information System' 카테고리의 다른 글
| [웹정보] ch06 Association Rules2 (0) | 2024.04.20 |
|---|---|
| [웹정보] ch06 Association Rules1 (0) | 2024.04.20 |
| [웹정보] ch05 Link Analysis2 (0) | 2024.04.16 |
| [웹정보] ch05 Link Analysis1 (0) | 2024.04.15 |
| [웹정보] ch03 Finding Similar Items1 (0) | 2024.03.15 |



