Chapter05 Link Analysis
Page Rank
Simple flow page model:
페이지 P는 중요도를 outlink에게 N등분 한다.

위처럼 3개의 미지수, 3개의 식으로는 유니크한 값이 나오지는 않아서 아래와 같은 식을 추가하면 값을 보일 수 있음.
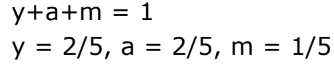
Matrix formulation:
행렬 M은 웹페이지 개수 x 웹페이지 개수 형태임.
i와 j가 연결 안되어 있으면 Mij = 0, 연결되어있으면 Mij = 1/n
따라서 M은 stochastic matrix임. -> 매 column의 값들을 더하면 1이 됨.
r은 랭크 벡터. ri는 page i의 중요도 점수이다.


이므로 랭크 벡터 r은 eigenvector가 되고, 1은 M의 eigenvalue가 된다.

Power Iteration:
- 초기값: r0 = [1/N,...,1/N]^T
- 반복:r(k+1) = Mr^k
- 종료점: |r(k+1) - rk| < ε

Random Walk Interpretation:
random sufer는 t시간에 페이지 P 위에있고, t+1시간이 되면 outlink를 타고 랜덤하게, uniformly하게 다른페이지로 간다.
p(t)를 t시간에 i페이지에 random sufer가 있을 확률이라고 하자.
t+1시간에는 surfer가 어디에 존재할까?
p(t+1) = Mp(t)가 된다.
p(t+1) = Mp(t) = p(t)라고 가정하자. 이때 p(t)는 stationary distribution, 수렴하는 확률에 도달한다.
(방문횟수의 비율이 특정 확률분포로 수렴하게 되고 우리는 이 분포를 stationary distribution이라 부른다.)
이는 사실 Markov processes의 결과이다! 이게 뭐냐면!
특정 조건을 만족한다면(주기성이 없고, 모든 길이 있고(connect well)),
어떤 초기값이든 간에 반드시 unique solution에 도달한다!
Spider traps:
한 그룹의 페이지들이 외부로 나가는 링크를 가지고 있지 않는 경우를 말한다.
spider trap에 들어가면 그 밖으로 나가지를 못할 수 있어 unique solution에 도달하지 못한다.
random walk의 조건 위배!
아래의 예시에서는 Microsoft가 spider trap이됨.

Random teleport:
이건 spider trap을 빠져나오기 위해 google이 제안한 방법임.
각 time step에서 random surfer는 아래의 두 옵션 중 하나를 선택함.
- 확률 β로 무작위로 링크를 따라 이동.
- 확률 1-β로 무작위로 페이지 중 하나로 텔레포트.(링크 상관 x)
β값은 주로 0.8~0.9사이의 값임. 0.2~0.1확률로 랜덤 텔레포트를 함.
아래는 랜덤 텔레포트의 예시.
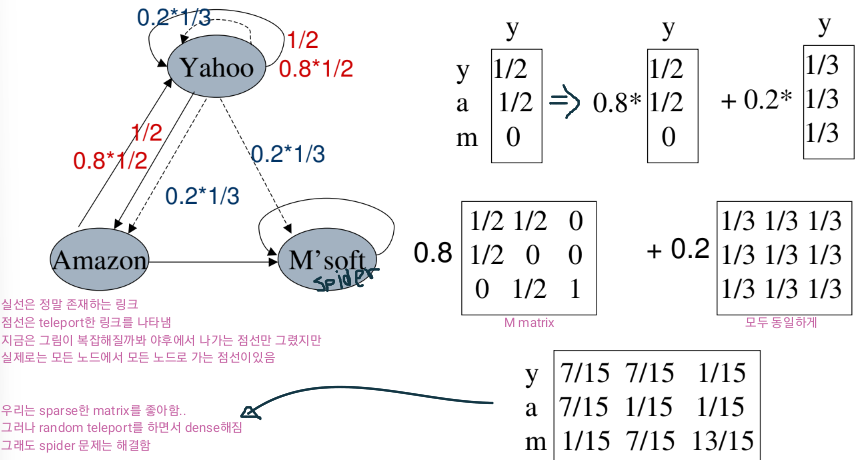

????????? 0..84가 이해가 안간당..
앞에서는 계속 r = Mr 로 했다면 앞으로는 random teleport로 구한 A 행렬이 M을 대신해 r = Ar로 계산한다!
(A계산은 한번만 하면 되는 것임!!)
A를 수식으로 나타내면 아래와 같고, A는 stochastic한 행렬이다.

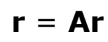

Dead ends:
막다른 길. 다음 스텝으로 나갈 수 없음.
아래와 같은 상황을 dead-end 상황이라고 한다.

그럼 dead-end는 어떻게 해결해야 할까?
- Sol1. Teleport
- Sol2. Prune & propagate (가지치기와 전파)
- dead-end인 애를 잘라냄
- 잘린 애들의 rank값을 전파함
Computing page rank:
다시한번 페이지 랭크를 구하는 식을 정리하면 아래와 같다.

N = 1 billion(10^9) 페이지를 가지고 있다하자.
각 엔트리는 4 byte가 필요하고, N^2개의 엔트리가 있으니까
4*10^18byte = (4GB)^2 -> 0이 18개
→ 우리는 희소행렬을 사용해서 메모리를 효율적으로 사용해야 함!
식을 아래처럼 재정비해보자

dense한 행렬 A 대신 sparse한 M으로 r을 나타낸 것임.
아깐 N^2이라 0이 18개이었지만,
만약 노드 당 10개의 링크가 있다면 10N이므로 0이 10개가 됨. -> 4*10*10^9 = 40GB

Basic Algorithm:
r(old)와 M은 disk에 저장되어있고, r(new)가 들어올만큼의 충분한 RAM이 있다고 하자.
◇ 초기화:

◇ 반복:

우리는 매 반복마다 아래의 연산을 해야해서
- r(old)와 M을 읽어와야 하고
- r(new)를 disk에 다시 써야함
입출력 비용은 2|r| + |M|이다.
고려해야할 사항은 아래와 같다
- 우리가 r(new)와 r(old)를 둘 다 저장할 만큼 충분한 메모리가 있다면?
- 우리가 r(new)를 저장할 만큼의 메모리가 없다면?
Block-based update Algorithm:
위의 고려 사항의 흐름에서 나온 방법이다.
만약 r(new)를 다 올릴 수 있는 상황이 아니라면 이 방법을 사용할 수 있다.

0,1 블록만 메인메모리에 올라옴 -> M테이블에서 src0부터 src2까지 순차적으로 r(new)에 업데이트
0,1 블록 내려가고 2,3 블록 메인메모리에 올라옴 -> M테이블에서 src0부터 src2까지 순차적으로 r(new)에 업데이트
. . .
이렇게하면 블록의 개수가 k개일 때 계산 비용은 아래와 같음
k(|M| + |r|) + |r| = k|M| + (k+1)|r|
어떻게 하면 더 잘 할 수 있을까?
Hint: M은 r보다 훨씬 크다. 그래서 k번 읽는 것을 방지해야 한다.
Block-Stripe update Algorithm:
너무 큰 M을 좀 덜 읽을 수는 없을까? 해서 나온 아이디어이다.

0,1블럭을 볼 때 destination에 0과 1만 있도록 만든다.
여기서의 계산비용은 아래와 같다.

위의 Block-based update Algorithm의 계산 비용 식과 비교하면 바로 이해가능하다.
여기서 엡실론 값은 테이블을 쪼개는 등의 추가적인 연산이다.
내가 여기에 이 경우 degree를 가지고 있어야한다고 썼는데 이거뭘깡????
'Computer Science > Web Information System' 카테고리의 다른 글
| [웹정보] ch06 Association Rules2 (0) | 2024.04.20 |
|---|---|
| [웹정보] ch06 Association Rules1 (0) | 2024.04.20 |
| [웹정보] ch05 Link Analysis2 (0) | 2024.04.16 |
| [웹정보] ch03 Finding Similar Items2 (0) | 2024.03.25 |
| [웹정보] ch03 Finding Similar Items1 (0) | 2024.03.15 |



